(Sample) 3rd order Sallen-Key High-pass Filter Design Tool - Result -
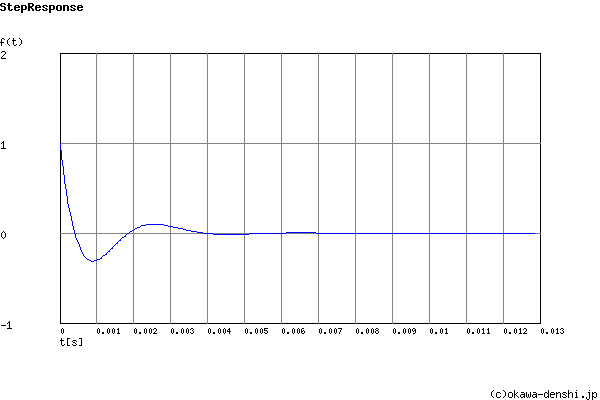
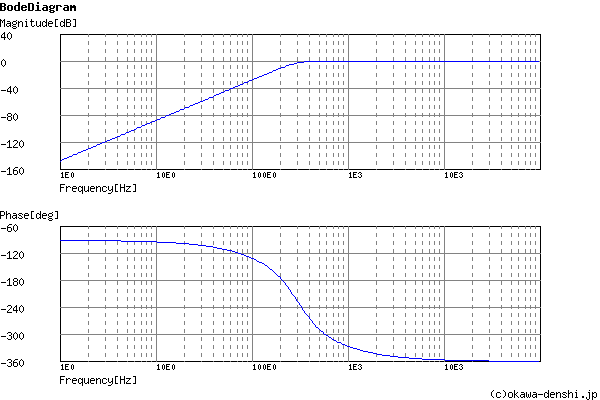
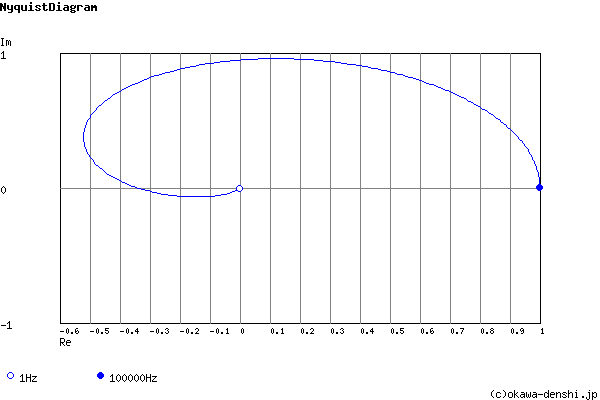
Calculated the Transfer Function for the 3rd order Sallen-Key High-pass filter, displayed on graphs, showing Bode diagram, Nyquist diagram, Impulse response and Step response.
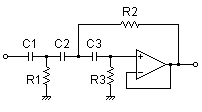
3rd order Sallen-Key filter
| Vi→ |
|
→Vo |
| G(s)= |
s3 s3+3710.78431373s2+7087418.30065s+6808278867.1 |
R1 = 5.1kΩ
R2 = 24kΩ
R3 = 120kΩ
C1 = 0.1uF
C2 = 0.01uF
C3 = 0.01uF
Equivalent block diagram:
| Vi(s)→ | 2πfc1 s+2πfc1 | → | (2πfc2)2 s2+2ζ(2πfc2)s+(2πfc2)2 | →Vo(s) |
Cut-off frequency fc1, fc2 of equivalent block diagram:
fc1 = 297.268553162[Hz]
fc2 = 303.860592855[Hz]
Damping ratio ζ of equivalent block diagram:fc2 = 303.860592855[Hz]
ζ = 0.482657376462
Pole(s)
p = -146.660556558 +266.123920459i[Hz]
|p|= 303.860592855[Hz]
p = -297.268553162[Hz]
|p|= 297.268553162[Hz]
p = -146.660556558-266.123920459i[Hz]
|p|= 303.860592855[Hz]
|p|= 303.860592855[Hz]
p = -297.268553162[Hz]
|p|= 297.268553162[Hz]
p = -146.660556558-266.123920459i[Hz]
|p|= 303.860592855[Hz]
Zero(s)
z = 0[Hz]
|z|= 0[Hz]
z = -0[Hz]
|z|= 0[Hz]
z = -0[Hz]
|z|= 0[Hz]
|z|= 0[Hz]
z = -0[Hz]
|z|= 0[Hz]
z = -0[Hz]
|z|= 0[Hz]
Phase margin
pm= NAN[deg] (f =0[Hz])
Oscillation frequency
f = 266.123920459[Hz]
Overshoot (in absolute value)
The 1st peak gpk = -0.32 (t =0.00088[sec])
The 2nd peak gpk = 0.1 (t =0.0025[sec])
The 3rd peak gpk = -0.017 (t =0.0045[sec])
The 2nd peak gpk = 0.1 (t =0.0025[sec])
The 3rd peak gpk = -0.017 (t =0.0045[sec])
Final value of the step response (on the condition that the system converged when t goes to infinity)
g(∞) = 0
Frequency analysis
Transient analysis