OKAWA Electric Design
English  |  Japanese

(Sample) Feedback system using a Transfer Function Analysis and Design Tool - Result -


(Sample) Transfer Function from the feedback system:
C
R 		= 10000s2+1000000000s+1000000000000
s3+11000s2+1100000000s+1000000000000

Pole(s)

p = -5041.6022387124 +32639.516083246i
      |p|= 5256.3453320825[Hz]
p = -916.79552257527
      |p|= 145.91253922237[Hz]
p = -5041.6022387124-32639.516083246i
      |p|= 5256.3453320825[Hz]

Zero(s)

z = -1010.2051443364
      |z|= 160.77914225801[Hz]
z = -98989.794855664
      |z|= 15754.715166932[Hz]

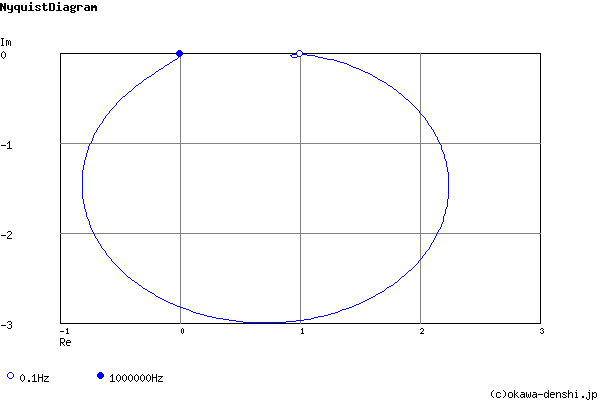
Phase margin

pm= 49.7[deg] (f =7256.9[Hz])

Oscillation frequency:

f = 5194.7403247761[Hz]

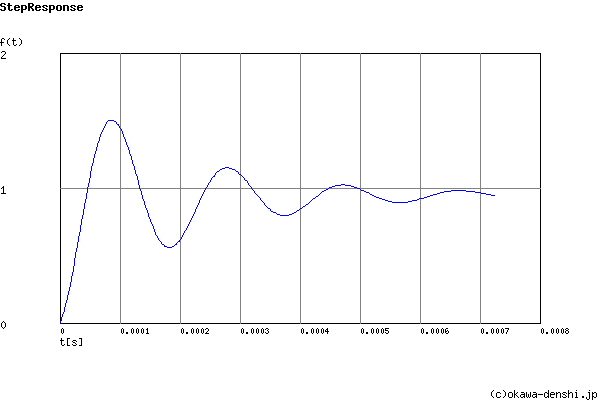
Overshoot (in absolute value)

The 1st peak  gpk = 1.5 (t =8.7E-5[sec])
The 2nd peak  gpk = 0.56 (t =0.00018[sec])
The 3rd peak  gpk = 1.15 (t =0.00028[sec])

Final value of the step response (on the condition that the system converged when t goes to infinity)

g(∞) = 1

Select the following System:

Gβ=
Gα=

Hβ=
Hα=

H2β=
H2α=

Frequency analysis

Bode diagram
    Phase  Group delay
Nyquist diagram(f =0→∞)
Pole, zero
Phase margin
Oscillation analysis

Upper and lower frequency limits:
  f1= - f2=[Hz] (frequency limits are optional)

Transient analysis

Step response
Impulse response
Overshoot
Final value of the step response

Simulation time:
  0〜[sec] (optional)



Frequency analysis

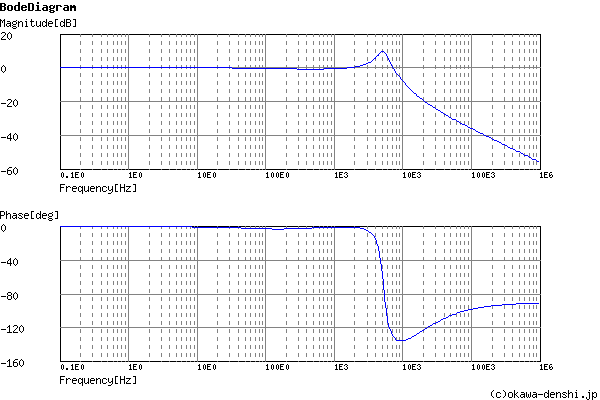
Gain characteristics at the Bode Diagram (provides up to 1 minute)

Phase characteristics at the Bode Diagram (provides up to 1 minute)

Bode Diagram text data (provides up to 1 minute)






Nyquist Diagram text data (provides up to 1 minute)


Transient analysis





Step Response text data (provides up to 1 minute)