減衰比ζ
2次遅れの伝達関数の一般式が次の式2-3-30のように与えられているとき式中のζ が減衰比(damping ratio)です.
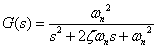
|
式2-3-30 |
減衰比ζ は2次系伝達関数の振動の大きさを示すパラメータです.ζ の数値範囲別に伝達関数の特徴を示すと下表の通りです.
| 減衰比ζ | 応答 | 説 明 |
| |ζ|< 1 | 不足減衰 | G(s)は振動系で,|ζ| が小さいほど振動の振幅が大きくなります. |
| |ζ|= 1 | 臨界減衰 | G(s)は非振動系です.非振動系の条件では最も,STEP応答などの過渡の応答において立ち上がり時間が小さくなります. |
| |ζ|> 1 | 過減衰 | G(s)は非振動系です.|ζ| が大きいほど,STEP応答などの過渡の応答において立ち上がり時間が大きく(鈍い応答に)なります |
式2-3-30において,ωnは固定角周波数といいます.G(s)伝達関数の周波数応答において,与えられる角周波数がこの固定角周波数ωnである場合,G(jωn)のゲインは,s=jωとして(伝達関数のフーリエ変換参照)ωにωnを代入すると次式が得られます.
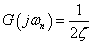
この式からζ は固定角周波数ωnにおける伝達関数のゲインを設定していることにもなります.