(サンプル)Sallen-Key 3次ローパス・フィルタ計算ツール
Sallen-Key 3次ローパス・フィルタの伝達関数を求め,その伝達関数の各種応答について計算します.
Sallen-Key 3次フィルタ
| Vi→ |
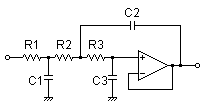
|
→Vo |
| G(s)= |
124195491660 s3+6396.73152121s2+50120332.6144s+124195491660 |
R1 = 51kΩ
R2 = 82kΩ
R3 = 39kΩ
C1 = 0.0068uF
C2 = 0.022uF
C3 = 330pF
等価ブロック線図:
| Vi(s)→ | 2πfc1 s+2πfc1 | → | (2πfc2)2 s2+2ζ(2πfc2)s+(2πfc2)2 | →Vo(s) |
等価ブロック線図における遮断周波数(カットオフ周波数)
fc1 = 495.420147192[Hz]
fc2 = 1005.30138528[Hz]
等価ブロック線図における減衰比ζfc2 = 1005.30138528[Hz]
ζ = 0.259947564828
極
p = -261.325647021 +970.741871687i[Hz]
|p|= 1005.30138528[Hz]
p = -495.420147192[Hz]
|p|= 495.420147192[Hz]
p = -261.325647021-970.741871687i[Hz]
|p|= 1005.30138528[Hz]
|p|= 1005.30138528[Hz]
p = -495.420147192[Hz]
|p|= 495.420147192[Hz]
p = -261.325647021-970.741871687i[Hz]
|p|= 1005.30138528[Hz]
位相余裕
pm= NAN[deg] (f =0[Hz])
過渡波形に含まれる振動周波数は
f = 970.741871687[Hz]
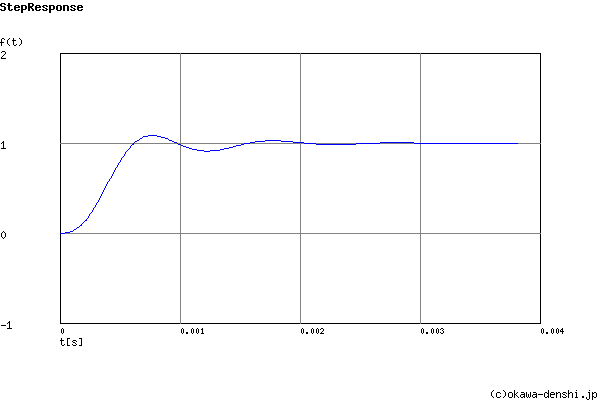
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = 1.05 (t =0.00078[sec])
第2ピーク gpk = 0.91 (t =0.0012[sec])
第3ピーク gpk = 1.02 (t =0.0018[sec])
第2ピーク gpk = 0.91 (t =0.0012[sec])
第3ピーク gpk = 1.02 (t =0.0018[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1
周波数解析
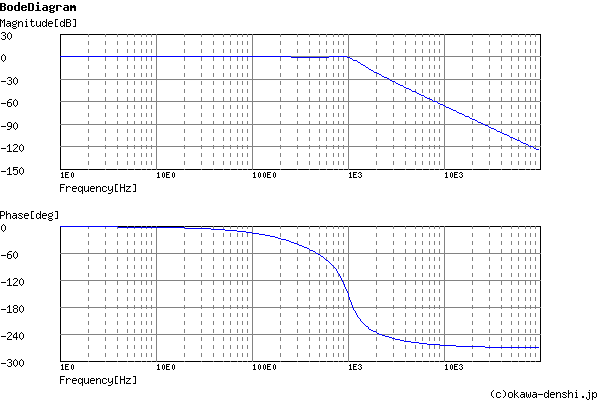
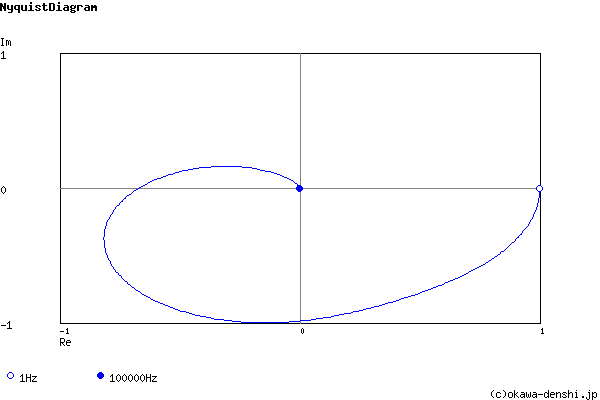
過渡解析