(サンプル)伝達関数計算ツール
伝達関数の各種応答
(サンプルの)伝達関数:
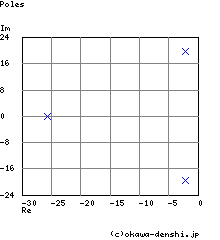
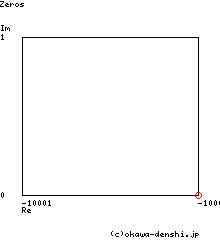
| G(s)= |
s+10000 s3+30s2+500s+10000 |
s平面上の極
p = -2.1552679847381 +19.611717445798i
|p|= 3.1400937168562[Hz]
p = -25.689464030524
|p|= 4.0886051858393[Hz]
p = -2.1552679847381-19.611717445798i
|p|= 3.1400937168562[Hz]
|p|= 3.1400937168562[Hz]
p = -25.689464030524
|p|= 4.0886051858393[Hz]
p = -2.1552679847381-19.611717445798i
|p|= 3.1400937168562[Hz]
s平面上の零点
z = -10000
|z|= 1591.549430919[Hz]
|z|= 1591.549430919[Hz]
位相余裕
pm= -21[deg] (f =4[Hz])
過渡波形に含まれる振動周波数は
f = 3.1213017740203[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = 1.55 (t =0.2[sec])
第2ピーク gpk = 0.61 (t =0.36[sec])
第3ピーク gpk = 1.28 (t =0.52[sec])
第2ピーク gpk = 0.61 (t =0.36[sec])
第3ピーク gpk = 1.28 (t =0.52[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1
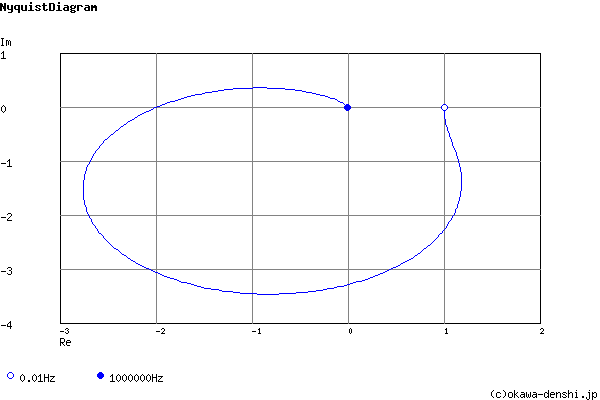
周波数解析
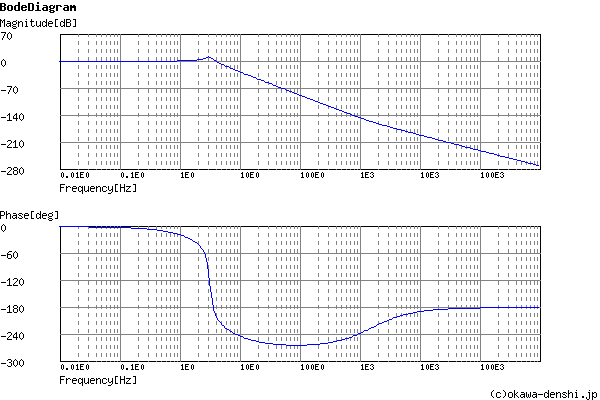
Gain characteristics at the Bode Diagram (寿命1分程度)
Phase characteristics at the Bode Diagram (寿命1分程度)
Bode Diagram text data (寿命1分程度)
過渡解析