Transfer Function Analysis and Design Tools
This page is a web application that simulate a transfer function.The transfer function is simulated frequency analysis and transient analysis on graphs, showing Bode diagram, Nyquist diagram, Impulse response and Step response.
And use this utility to design the transfer function at a given some poles and zeros or other paramaters.
Transfer Function:
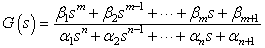
The following form is an example to input G(s). Use the right form to simulate.
β=
α=
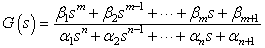
Transient analysis condition is n≥m. maximum n=12
Example
| G(s)= |
10000 s2+50s+10000 |
β=
α=