(Sample) 3rd order Multiple Feedback Low-pass Filter Design Tool

English | Japanese

(Sample) 3rd order Multiple Feedback Low-pass Filter Design Tool - Result -

Calculated the Transfer Function for the 3rd order Multiple Feedback Low-pass filter, displayed on graphs, showing Bode diagram, Nyquist diagram, Impulse response and Step response.

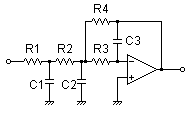
3rd order Multiple Feedback Filter

Vi→

→Vo

(Sample)Transfer function:

G(s)=

-79063161.7478

s³+466.724312356s²+392148.494742s+80593959.1348

R1 = 910Ω
R2 = 47kΩ
R3 = 130kΩ
R4 = 47kΩ
C1 = 4.7uF
C2 = 0.22uF
C3 = 0.0022uF

Equivalent block diagram:

Vi(s)→

2πfc1

s+2πfc1

→

(2πfc2)²

s²+2ζ(2πfc2)s+(2πfc2)²

→Vo(s)

Cut-off frequency fc1, fc2 of equivalent block diagram:
    fc1 = 37.9811225476[Hz]
    fc2 = 92.4905889032[Hz]

Damping ratio ζ of equivalent block diagram:
    ζ = 0.196238121389

Pole(s)
    p = -18.1501794125 +90.6922269158i[Hz]
          |p|= 92.4905889032[Hz]
    p = -37.9811225476[Hz]
          |p|= 37.9811225476[Hz]
    p = -18.1501794125-90.6922269158i[Hz]
          |p|= 92.4905889032[Hz]

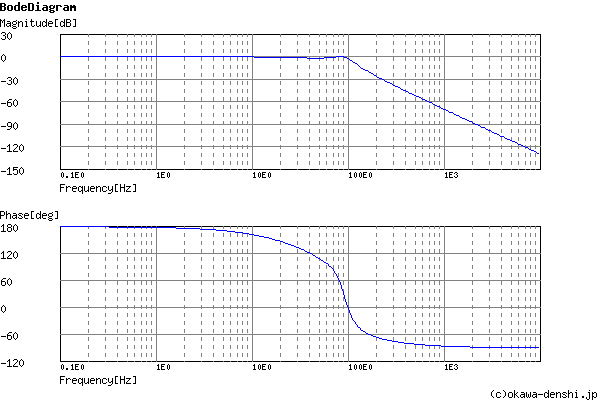
Phase margin
    pm= 214[deg] (f =89[Hz])

Oscillation frequency
    f = 90.6922269158[Hz]

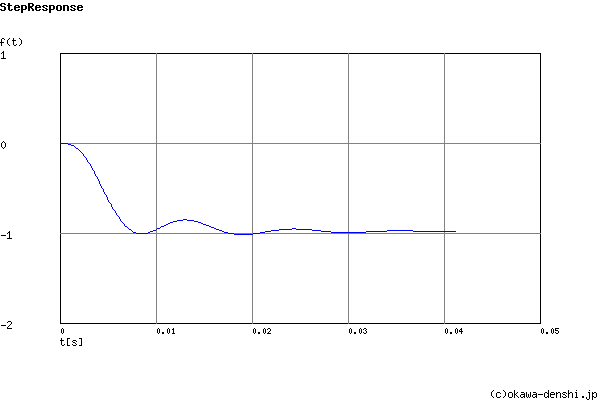
Overshoot (in absolute value)
    The 1st peak  g_pk = -1.01 (t =0.0085[sec])
    The 2nd peak  g_pk = -0.85 (t =0.013[sec])
    The 3rd peak  g_pk = -1.02 (t =0.019[sec])

Final value of the step response (on the condition that the system converged when t goes to infinity)
    g(∞) = -0.981006053016

Filter gain at f=0Hz:
K=Times (K<0)

Select filter type Set parameters of the equivalent block diagram

1st filter:
f_c1=Hz
2nd filter:
f_c2=Hz	Damping ratio ζ=

Butterworth filter

Cut-off frequency fc=Hz

Chebyshev filter

Characteristic frequency: fc=Hz
Gain ripple: gr=dB

C1 = F

C2 = F

C1, C2 is optional. But when setting these capacitances, C1 and C2 of both are needed.

Select Capacitor Sequence:
Select Resistor Sequence:

Frequency analysis Bode diagram
Phase Group delay
Nyquist diagram
Pole, zero
Phase margin
Oscillation analysis
Analysis on frequency range:
f1=∼f2=[Hz] (optional)

Transient analysis Step responseImpulse response
Overshoot
Final value of the step response
Analysis on time range:
0∼[sec] (optional)

Frequency analysis

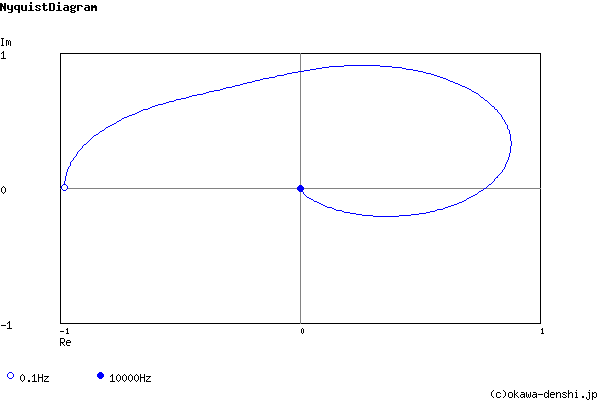
Transient analysis

Top