OKAWA Electric Design
English  |  Japanese

(Sample)Multiple Feedback High-pass Filter Design Tool - Result -

Calculated the Transfer Function for the multiple feedback high-pass filter, displayed on graphs, showing Bode diagram, Nyquist diagram, Impulse response and Step response.

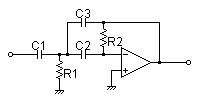
Multiple Feedback Filter

Vin(s)→ →Vout(s)
(Sample)Transfer Function:
G(s)= -1s2
s2+2941.17647059s+4368949.00563


R1 = 3.3kΩ
R2 = 15kΩ
C1 = 0.068uF
C2 = 0.068uF
C3 = 0.068uF

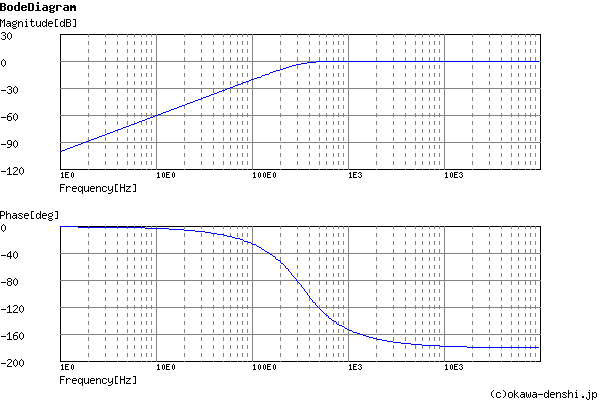
Cut-off frequency

fc = 332.666155674[Hz]

Gain at f=∞Hz

Gpk = -1[times] (0)[dB]

Quality factor

Q = 0.710669054519

Damping ratio

ζ = 0.703562363974

Pole(s)

p = -234.0513869 +236.40372125i[Hz]
  |p|= 332.666155674[Hz]
p = -234.0513869-236.40372125i[Hz]
  |p|= 332.666155674[Hz]

Zero(s)

z = 0[Hz]
  |z|= 0[Hz]
z = -0[Hz]
  |z|= 0[Hz]

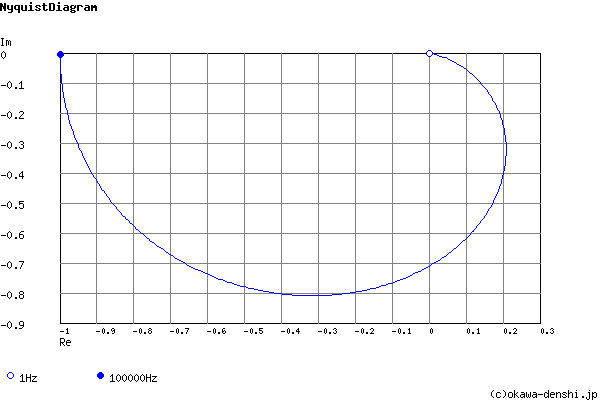
Phase margin

pm= NAN[deg] (f =0[Hz])

Oscillation frequency

f = 236.40372125[Hz]

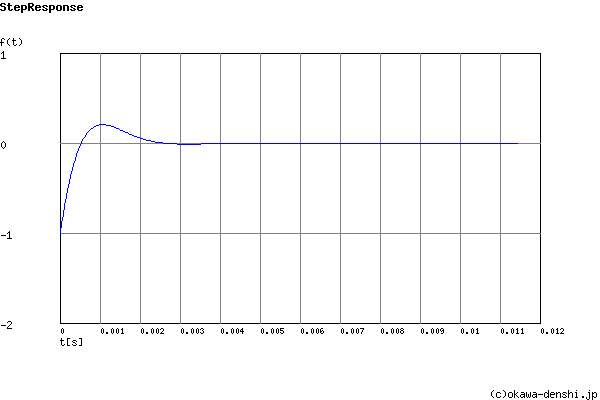
Overshoot (in absolute value)

The 1st peak  gpk = 0.21 (t =0.0011[sec])
The 2nd peak  gpk = -0.0093 (t =0.0032[sec])
The 3rd peak  gpk = 0.00042 (t =0.0053[sec])

Final value of the step response (on the condition that the system converged when t goes to infinity)

g(∞) = 0

fc=Hz
Gain K= at f=0Hz (K<0)

Q factor | Damping ratio ζ

Quality factor Q =
Damping ratio ζ =
C1 =F C2 =F C3 =F
C1, C2, C3 is optional. But when setting these capacitances, C1, C2 and C3 of all are needed to give, and K setting is ignored.

Select Capacitor Sequence:
Select Resistor Sequence:

Frequency analysis

Bode diagram
    Phase  Group delay
Nyquist diagram
Pole, zero
Phase margin
Oscillation analysis
Analysis on frequency range:
  f1=∼f2=[Hz] (optional)

Transient analysis

Step response
Impulse response
Overshoot
Final value of the step response
Analysis on time range:
  0∼[sec] (optional)


Frequency analysis





Transient analysis