OKAWA Electric Design
English  |  Japanese

(Sample)Multiple Feedback Low-pass Filter Design Tool - Result -

Calculated the Transfer Function for the multiple feedback low-pass filter, displayed on graphs, showing Bode diagram, Nyquist diagram, Impulse response and Step response.

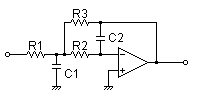
Multiple Feedback Filter

Vin(s)→ →Vout(s)
(Sample)Transfer Function:
G(s)= -39313739.3656
s2+12601.6260163s+39313739.3656


R1 = 8.2kΩ
R2 = 30kΩ
R3 = 8.2kΩ
C1 = 0.022uF
C2 = 0.0047uF

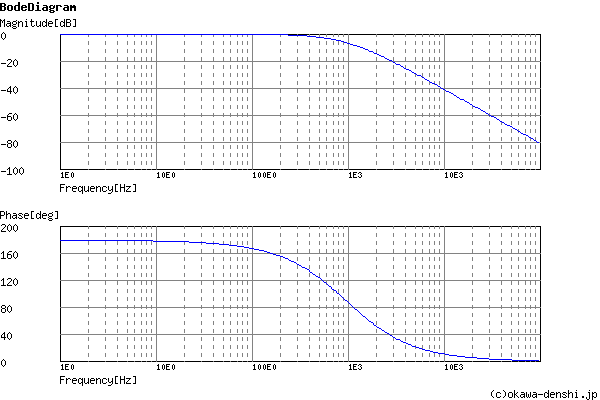
Cut-off frequency

fc = 997.912146175[Hz]

Gain at f=0Hz

Gpk = -1[times] (0)[dB]

Quality factor

Q = 0.497560150302

Damping ratio

ζ = 1.00490362762

Pole(s)

p = -903.859636226[Hz]
  |p|= 903.859636226[Hz]
p = -1101.75143526[Hz]
  |p|= 1101.75143526[Hz]

Phase margin

pm= NAN[deg] (f =0[Hz])

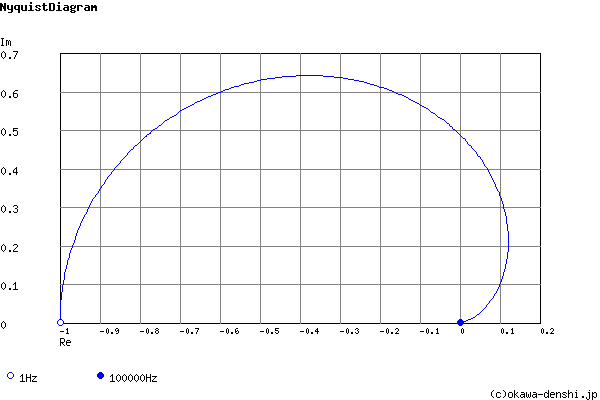
The system does not oscillate.

Overshoot (in absolute value)

The peak of transient waveform is not detected.

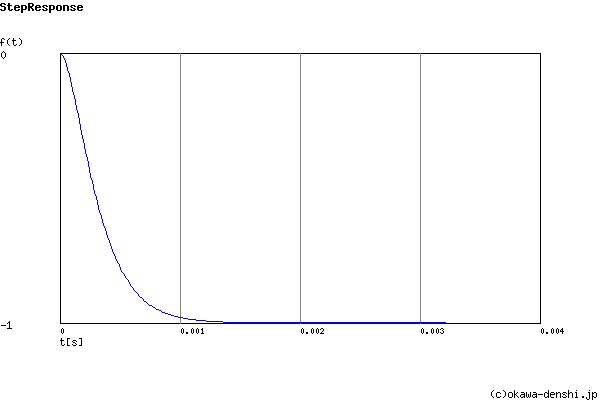
Final value of the step response (on the condition that the system converged when t goes to infinity)

g(∞) = -1

fc=Hz
Gain K= at f=0Hz. (K<0)

Q factor | Damping ratio ζ

Quality factor Q =
Damping ratio ζ =
C1 = F C2 = F
C1, C2 is optional. But when setting these capacitances, C1 and C2 of both are needed to give following the equation
(C2/C1)≤ζ 2/(1-K)
(C1/C2)≥Q2(1-K)

Select Capacitor Sequence:
Select Resistor Sequence:

Frequency analysis

Bode diagram
    Phase  Group delay
Nyquist diagram
Pole, zero
Phase margin
Oscillation analysis
Analysis on frequency range:
  f1=∼f2=[Hz] (optional)

Transient analysis

Step response
Impulse response
Overshoot
Final value of the step response
Analysis on time range:
  0∼[sec] (optional)


Frequency analysis





Transient analysis