(サンプル)オペアンプ多重帰還型バンドパス・フィルタ計算ツール
オペアンプ多重帰還型バンドパス・フィルタの伝達関数を求め,その伝達関数の各種応答について計算します.
オペアンプ多重帰還型フィルタ
| Vin(s)→ |
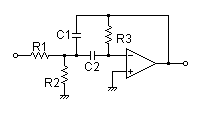
|
→Vout(s) |
| G(s)= |
-8912.65597148s s2+9238.72875092s+41335488.7073 |
R1 = 5.1kΩ
R2 = 20kΩ
R3 = 8.2kΩ
C1 = 0.022uF
C2 = 0.033uF
通過中心周波数
f0 = 1023.2498036[Hz]
通過中心周波数における利得
Gpk = -0.964705882353[倍] (-0.312101466612)[dB]
Q(クオリティ・ファクタ)
Q = 0.695903982559
減衰比ζ
ζ = 0.718489924661
極
p = -735.194674297 +711.70847364i[Hz]
|p|= 1023.2498036[Hz]
p = -735.194674297-711.70847364i[Hz]
|p|= 1023.2498036[Hz]
|p|= 1023.2498036[Hz]
p = -735.194674297-711.70847364i[Hz]
|p|= 1023.2498036[Hz]
零点
z = 0[Hz]
|z|= 0[Hz]
|z|= 0[Hz]
位相余裕
pm= NAN[deg] (f =0[Hz])
過渡波形に含まれる振動周波数は
f = 711.70847364[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = -0.63 (t =0.00017[sec])
第2ピーク gpk = 0.024 (t =0.00088[sec])
第3ピーク gpk = -0.00095 (t =0.0016[sec])
第2ピーク gpk = 0.024 (t =0.00088[sec])
第3ピーク gpk = -0.00095 (t =0.0016[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 0
周波数解析
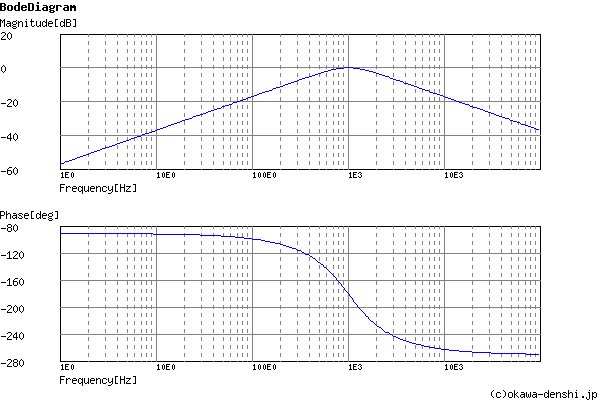
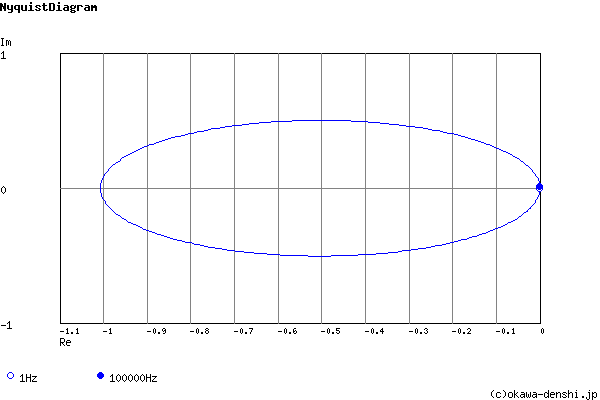
過渡解析