(サンプル)Twin-T CR・フィルタ計算ツール
Twin-T CRフィルタの伝達関数を求め,その伝達関数の各種応答について計算します.
| Vin(s)→ |
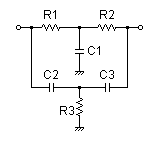
|
→Vout(s) |
| G(s)= |
s3+9090.90909091s2+41322314.0496s+368949232586 s3+36038.961039s2+284828807.556s+368949232586 |
R1 = 22kΩ
R2 = 22kΩ
R3 = 5.6kΩ
C1 = 0.01uF
C2 = 0.01uF
C3 = 0.01uF
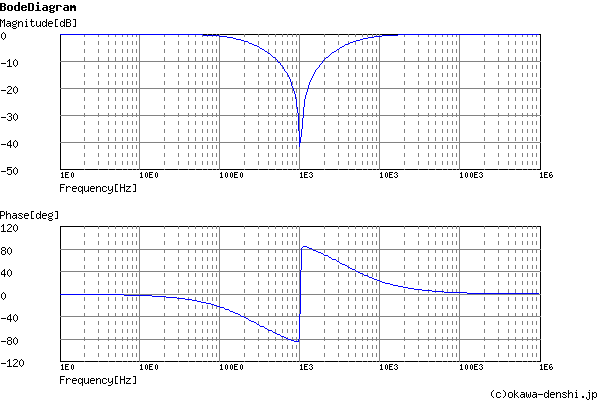
リジェクト周波数
f0 = 1023.08672291[Hz]
f0 = 1013.91087188[Hz]
※2式のリジェクト周波数 f0 が一致したときノッチフィルタとして機能します.
f0 = 1013.91087188[Hz]
※2式のリジェクト周波数 f0 が一致したときノッチフィルタとして機能します.
極
p = -255.895392582[Hz]
|p|= 255.895392582[Hz]
p = -4041.77097335[Hz]
|p|= 4041.77097335[Hz]
p = -1438.11242732[Hz]
|p|= 1438.11242732[Hz]
|p|= 255.895392582[Hz]
p = -4041.77097335[Hz]
|p|= 4041.77097335[Hz]
p = -1438.11242732[Hz]
|p|= 1438.11242732[Hz]
零点
z = -4.34076355049 +1016.95722029i[Hz]
|z|= 1016.96648427[Hz]
z = -1438.18159192[Hz]
|z|= 1438.18159192[Hz]
z = -4.34076355049-1016.95722029i[Hz]
|z|= 1016.96648427[Hz]
|z|= 1016.96648427[Hz]
z = -1438.18159192[Hz]
|z|= 1438.18159192[Hz]
z = -4.34076355049-1016.95722029i[Hz]
|z|= 1016.96648427[Hz]
位相余裕
pm= NAN[deg] (f =0[Hz])
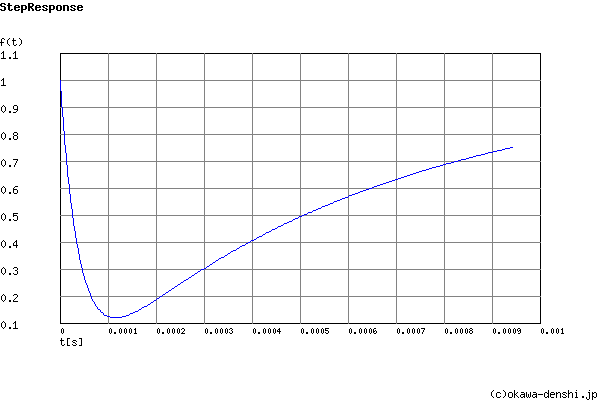
過渡波形に振動は含まれません.
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = 0.12 (t =0.00012[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1
周波数解析
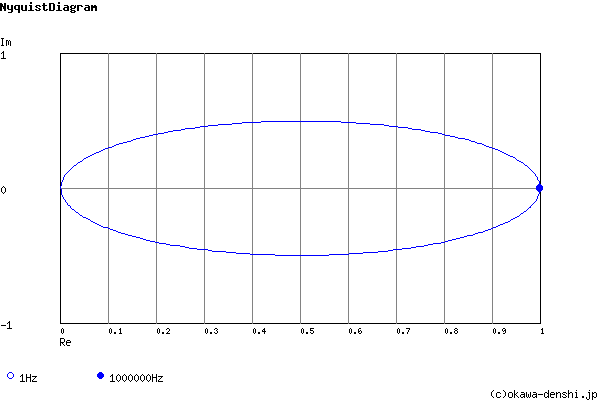
過渡解析