Multiple Feedback Band-pass Filter Design Tool
This page is a web application that design a multiple feedback band-pass filter. Use this utility to simulate the Transfer Function for filters at a given frequency, damping ratio ζ, Q or values of R and C. The response of the filter is displayed on graphs, showing Bode diagram, Nyquist diagram, Impulse response and Step response.
Calculate the transfer function for multiple feedback band-pass filter with R and C values
| Vin(s)→ |
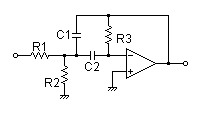
|
→Vout(s) |
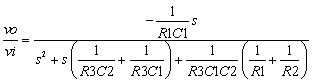
Calculate the R and C values for the multiple feedback filter at a given frequency and Q factor
| Vin(s)→ |

|
→Vout(s) |
Center frequency:
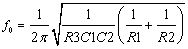
Transfer function:
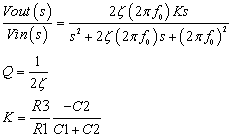
K is gain at the center frequency.